1. Elastic Constants in High Entropy Alloys (HEAs)
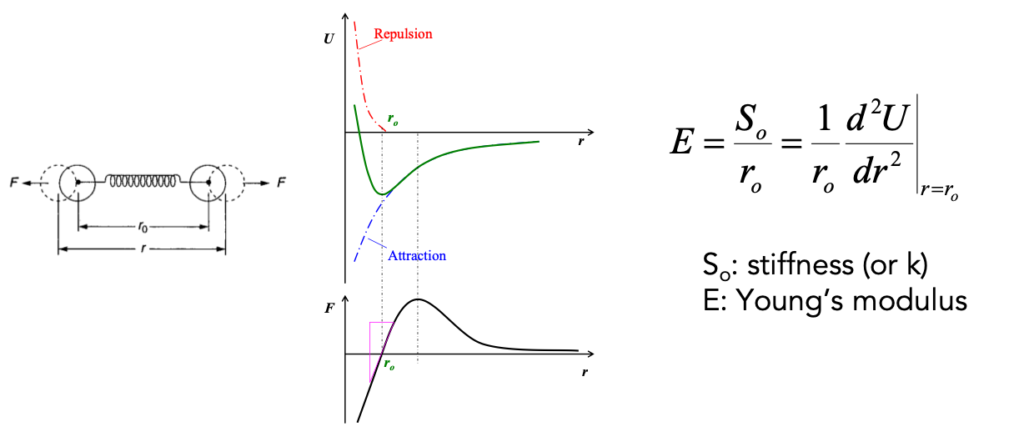
Elastic constants provide key insights on the mechanical behavior of materials. Bond strength is a critical descriptor of elastic constants. In a simple model, it can be used to determine Young’s modulus, E, of a material. It can be derived from the stiffness (So or k) of the bonds as shown below.
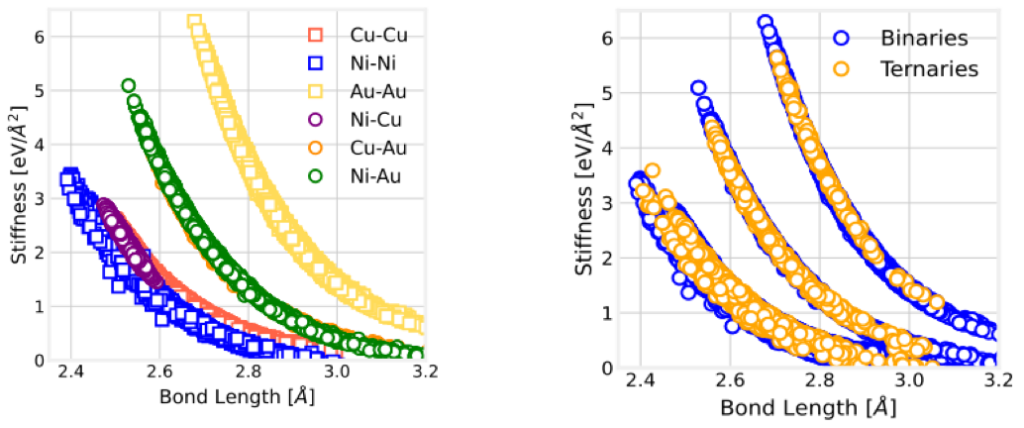
In our recent work in FCC solids, we showed that the force constant (k or bond stiffness) of a given A-B bond depends only on the bond length (see left figure below). The stiffness remains unchanged even in the presence of different nearest-neighbor elements, determined only by the bond length (see right figure).
We have used this relationship to develop a ML model that can predict elastic constants in high entropy bcc solids. Figure shows a very good comparison of Voigt-Reuss-Hill E (EVRH) between DFT and ML in ternary Ni-Cu-Au diagram. The model is trained on a DFT database using the PREDICT approach.
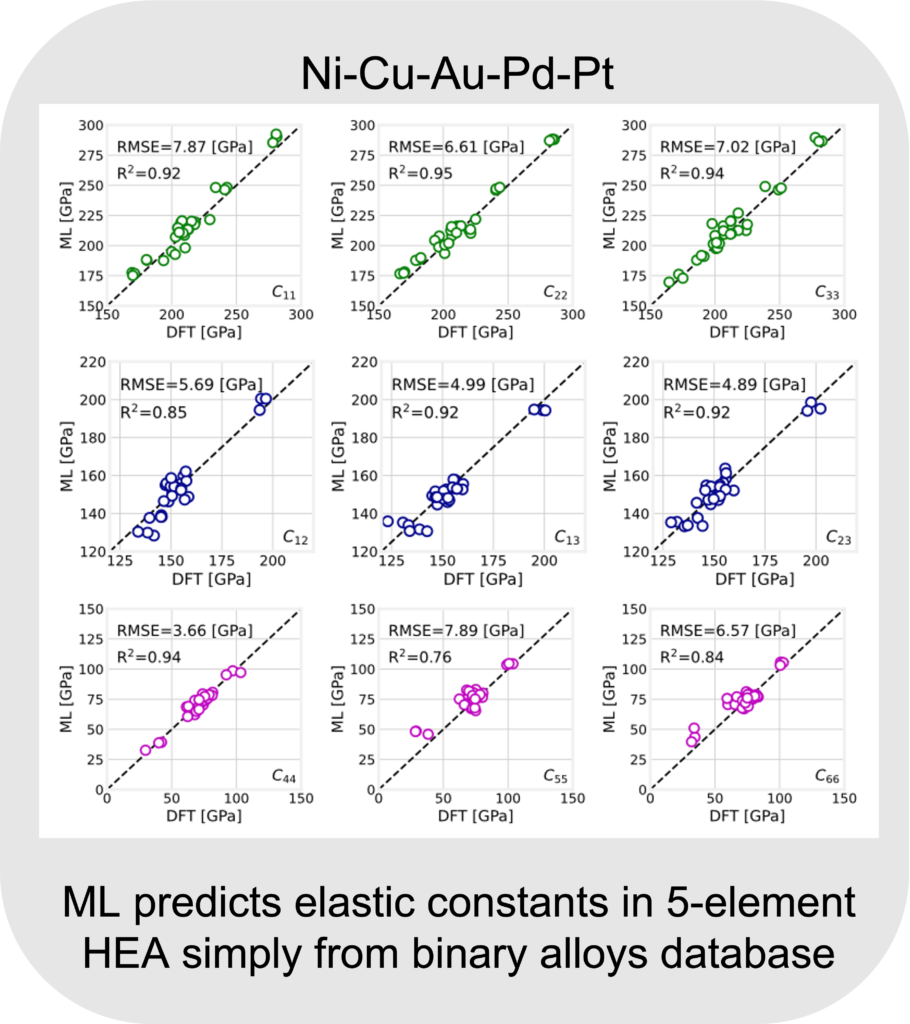
The ML predictions of elastic constants in five-element Ni-Cu-Au-Pd-Pt system is shown below. A very good comparison with DFT with an R2 > 0.85 for most and RMSE < 8 GPa is obtained indicating a good predictive capability of the model. For more info, refer Linton and Aidhy, A machine learning framework for elastic constants predictions in multi-principal element alloys, APL Machine Learning, 2022.
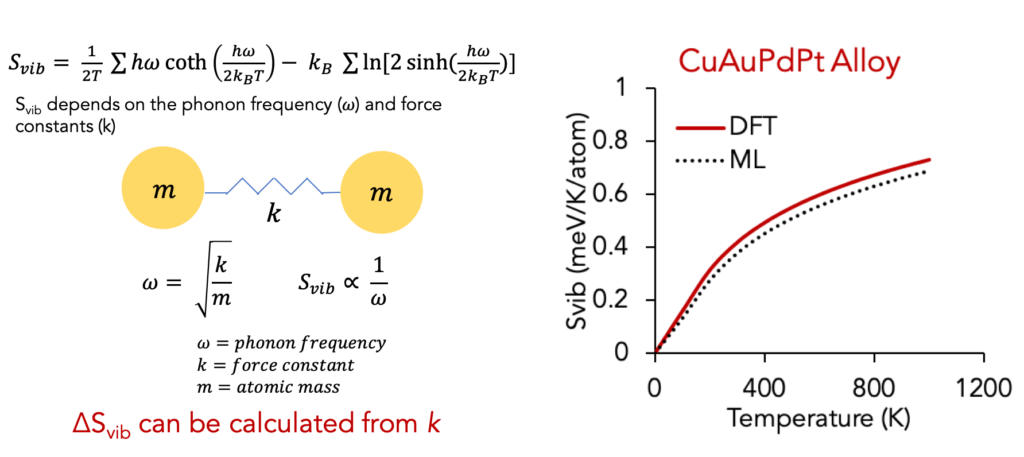
Interestingly, the same idea can also be used to predict thermodynamic quantities based on phonons. In particular, the vibrational entropy depends on the bond frequency and bond stiffness as shown in the relationships below.
This force constant-bond length relation can be used to predict vibrational entropy and the expensive phonon calculations can be completely bypassed. Above right figure shows a comparison of Svib from ML prediction vs DFT phonon explicit calculations.
2. Stacking Fault Energy (SFE) in HEAs
The co-presence of both high strength and high ductility is one of the most desired alloy properties. While a tradeoff between the two properties is normally observed in most alloys, the co-presence has been observed in multi principal element alloys (MPEAs) which has generated large interest in these alloys. Experimental investigations have revealed that the underlying cause is the change in the deformation mechanisms from slip to twinning. On the one hand, coherent twin boundaries act as barriers to dislocations, whereas on the other, they provide pathways for glide of dislocations. Formation of large number of twin boundaries is correlated to the stacking fault energy (SFE) of alloys, where it is observed that lowering the SFE favors twin formation. This lowering has been further tied to alloy composition that has opened a route to manipulate SFE. For example, it has been shown that SFE increases with Ni and Mn whereas it decreases with Co in FeCoNiCrMn. Similar trends for Ni and Co have also been observed in NiCoCr and various other alloys.
Despite these observations, due to the structural complexities and large compositional space in MPEAs, there is very little understanding of the guiding principles that drive the coupling between composition and SFE. As a result, tailoring SFE via composition remains an open challenge. However, over the years, the SFE-composition correlation has been widely investigated in dilute alloys. Density functional theory (DFT) has particularly aided to the atomic level understanding where the role of various elements in altering SFE of the host metal has been studied. A decrease of up to 100 mJ/m2 in Ni alloys due to various alloying elements has been reported. Similar studies have also been performed in Ir and Au in which both increase and decrease in SFEs depending on the choice of the alloying elements has been observed.
The explanation of the SFE trends due to alloying elements has been mainly provided using two variables, namely, the radius of the alloying element and the electronic charge. It has been postulated that there exists an inverse relationship between SFE and atomic radius of the alloying element. For example, it was shown that the SFE of Ni decreases linearly as the radius of the alloying element increases. However, the linearity is often found to accompany a large variation, i.e., despite similar atomic radii of two alloying elements, large SFE differences persist. Similarly, two alloying elements of widely different radii are found to result in similar SFEs. Our DFT calculations in Ni and Cu highlight a limited role of atomic radii to SFE. Figure shows SFE in doped Ni and Cu metals.
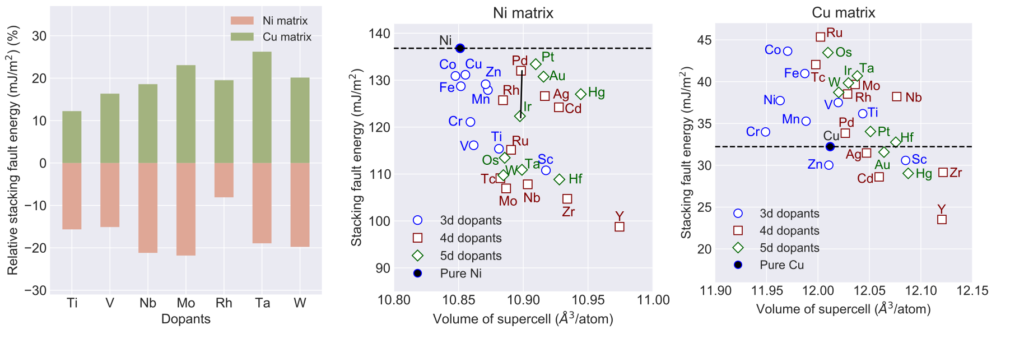
It is interesting to note the contrasting behavior between the two metals, i.e., while all alloying elements reduce SFE in Ni, it changes both ways in Cu. Based on the inverse relationship, the SFE decrease in Ni is understandable because it is the smallest atom among all elements. However, in Cu, some elements that are larger than Cu still result in higher SFE. Specifically, Ti, V, Nb, Mo, Rh, Ta and W have larger atomic radii than both Ni and Cu lead to SFE increase in Cu compared to the decrease in Ni. Thus, the inverse relationship does not seem to be a common guiding principle, at least in Ni and Cu. This is intriguing because both Ni and Cu are considered to be very similar elements from Hume-Rothery rules viewpoint.
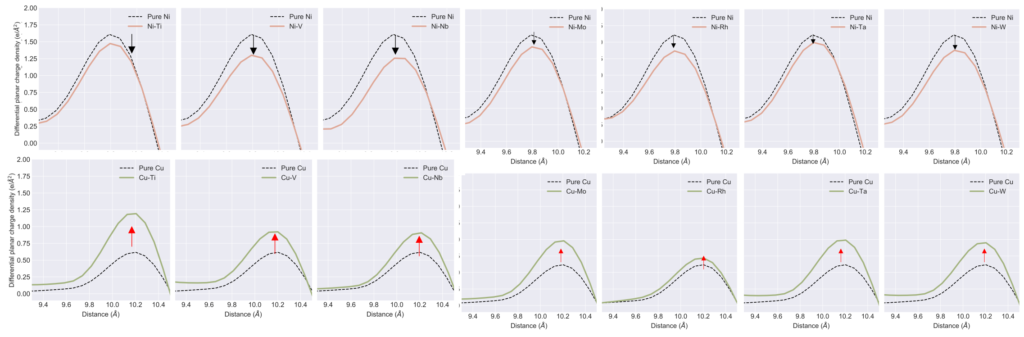
We find that charge density difference (i.e., charge density before and after shearing) is critical to SFE. Figure below shows that all those elements that raise SFE in Cu show an increase in charge density after shearing, making it harder to shear against the higher charge density. Opposite occurs in Ni. Thus, there is a resistance to shearing due to higher or unfavorable charge density that raises SFE.
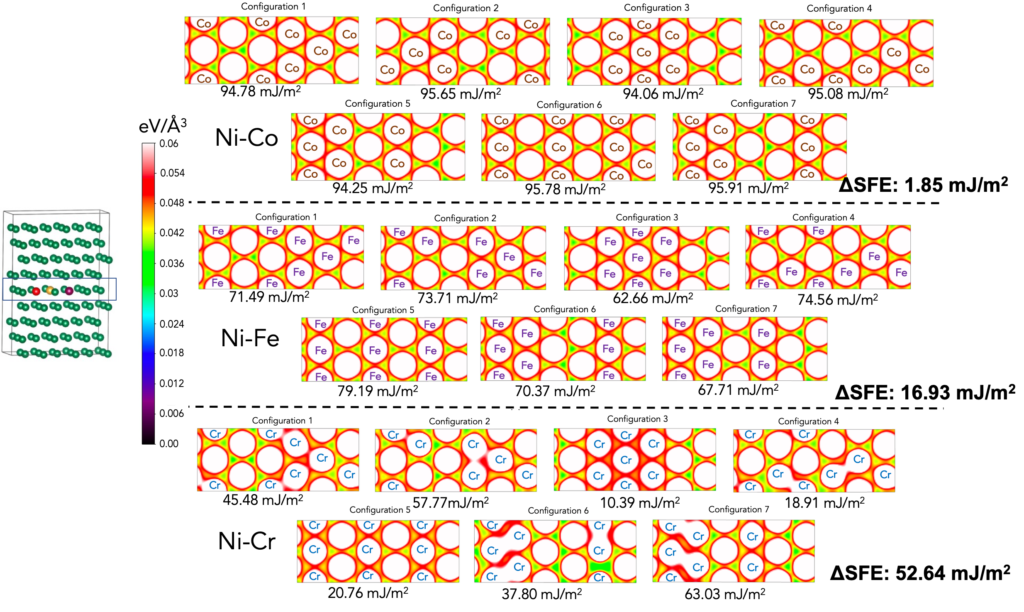
3. Charge density and SFE are strongly correlated
We have observed that charge density is strongly correlated to SFE. Below, seven different configurations in each of the three systems, i.e., Ni-Co, Ni-Fe and Ni-Cr are created. The charge densities of their shearing plane (see supercell and its highlighted plane) are plotted and the corresponding SFE values are also presented. Contrasting charge density distributions are observed between Ni-Co and Ni-Cr. It is observed that the charge density is very similar in all seven configurations in Ni-Co. In contrast, a large differences within the seven configurations of Ni-Cr are observed. The similarity in Ni-Co is represented in very little SFE differences (1.85 mJ/m2). Large dissimilarity in charge density distribution in Ni-Cr is revealed in its large SFE differences (52.64 mJ/m2).
Density of states (DOS) also reveal similar variations. DOS of Co/Cr atoms in each of four configurations of Ni-Co and Ni-Cr are shown. Very similar DOS are observed in Ni-Co compared to significant differences at the Fermi level in Ni-Cr.
In light of above, charge density is used to train a regression ML model to predict SFE in model HEAs. Figure shown predictions on quaternary Ni-based SFE.
4. Point Defect Energetics in HEAs and Predictions from ML
See Manzoor et al., Machine Learning Based Methodology to Predict Point Defect Energies in Multi-Principal Element Alloys, Frontiers on Materials, 8, 673574 (2021)
The chemical randomness results in unique nearest neighbor (NN) environments that cause lattice and electronic distortions. Recent experimental and computational studies reveal a wide distribution of bond lengths between any two A-B atoms depending upon their NN environments. The electronic charge distortion is revealed in different charge density distributions even of the same element depending on its NN environment. Because of different bonding environments, the radius of the same element has also been found to be different in previous studies depending on its NN environment. These distortions cause fluctuations in the energy landscape and result in a wide range of defect energies in contrast to a unique point-defect energy in pure/dilute materials. For example, in contrast to a unique vacancy formation energy in a pure or dilute metal, a distribution of more than 1 eV has been observed in NiCoCrFeMn. Consequently, it can lead to very unintuitive properties just with minor variations in the compositions.
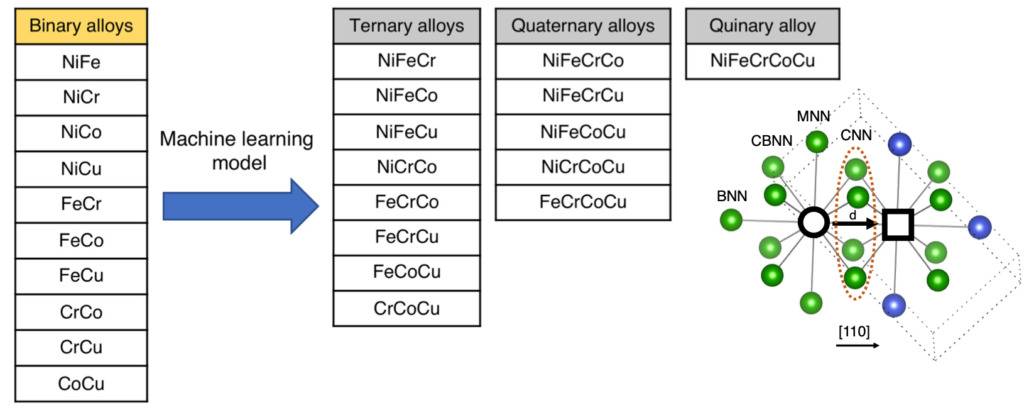
In order to trace the point defect energy landscape in HEAs, we have used the PREDICT approach in FCC solids to predict vacancy formation and migration energies. In the PREDICT approach, a DFT database of simpler/binary alloys is developed to train a ML model, which is then used to predict properties in complex/multi-elemental alloys. The descriptors are carefully incorporated. An example of the PREDICT approach applied to 5-element NiFeCrCoCu is shown below. Vectorial information of the NN descriptors are documented as shown in the lattice on the right figure.
The ML model enables vacancy formation and migration energies predictions. Below, left figure shows a comparison between ML predicted and LAMMPS calculated migration barriers. Using PREDICT approach, the phase space can be traced very quickly. The quality of predictions represented by R2 for the ternary diagram in NiFeCr is shown in figure on the right.
5. Vibrational entropy contribution to phase stability in concentrated alloys
to be added soon…(See paper – Manzoor et al., Entropy contributions to phase stability in binary random solid solutions, NPJ Computational Materials, 4, 47 (2018).