Previous:Contents 
Next: Input Files
Contents

---

I. INTRODUCTION

Numerical techniques have become a major force in the field of applied electromagnetics. The computing power of computers today has increased to such a large extent that analysis of complex problems is now possible through the use of numerical techniques. Some of the important techniques used are the Finite Element Method (FEM) [1], the Finite Difference Time Domain (FDTD) method [2], the Methods of Moments (MOM) [3] and the Transmission Line Matrix method (TLM).

The FEM and the FDTD methods are based on the solution of Maxwell's equations in their differential form (PDE techniques). These techniques are very good at modeling complex, inhomogeneous structures, but they have problems modeling open-region geometries. The MOM solves Maxwell's equations in an integral form (surface integral techniques). This technique is very good at solving open radiation problems but faces problems when it has to deal with complex geometries.

The finite element method is very popular in mechanical and civil engineering. It was first formulated for use in electromagnetics in the 1940's. Since then, it has come a long way. The introduction of vector (edge) elements [4] has greatly improved the performance of this technique. More recently, the application of the Perfectly Matched Layer (PML) concept to FEM [5] has enabled the analysis of open region problems. The FEM has also been successful when it has been hybridized with the MOM [6].

The FEM is a very versatile technique because it allows the analysis of complex structures. It has been used in a wide variety of problems like modeling waveguides and transmission lines, cavities etc. It also is computationally efficient because it yields sparse matrices. This thesis illustrates some of the advantages of using FEM by analyzing problems to which the FEM is easily applicable.

EMAP4 is three-dimensional code based on the vector (edge based) FEM. It also uses complex numbers, which enables it to analyze lossy structures. Perfectly matched layers have also been implemented in this code. The Complex Biconjugate Gradient (CBCG) method [7] is used to solve the matrix equation, making the code computationally efficient.

This thesis is organized in the following manner. Section II takes a brief look at the FEM formulation. Section III describes the use of this code and the description of keywords used to create the input files. Section IV describes the mesh generation in EMAP4. Section V describes the main subroutines in the code. Section VI outlines a few examples that illustrate the main applications of this code. The implementation of the PMLs is described in Section VII. Section VIII describes the application of sparse matrix routines to solve the matrix equation. Finally, Section IX summarizes the main points of the thesis and suggests future directions for the development of this code.
 
 
II. FEM FORMULATION IN THE EMAP4 CODE
 

The FEM formulation in EMAP4 starts with the three-dimensional wave equation

(1)

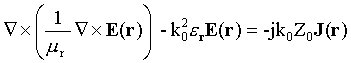
with boundary conditions given by

(2)

After multiplying Eq. (2.1) by a weighting function w(r) and integrating over the finite element volume V, one obtains the FEM weak form as follows:

. (3)

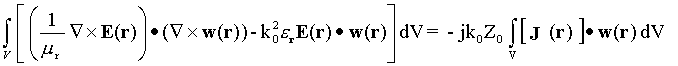
Tetrahedral elements are used to discretize the volume V. Basis functions are defined within a tetrahedron and are associated with one of the six edges [8]. Basis functions w_k(r) are defined as follows:

(4)

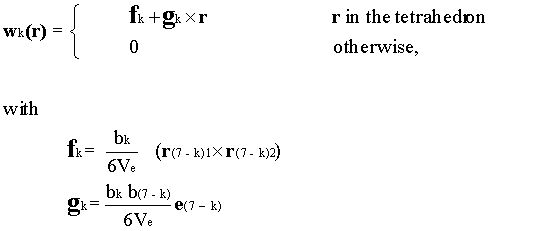
where k=1,2,…,6 and

V_e = volume of the tetrahedron,

e_k = unit vector of the kth edge,

b_k = length of the kth edge.

The electric field E within volume V can be expanded as:

(5)

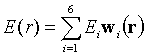
where {E_n} is a set of unknown complex scalar coefficients.

Using the Galerkin approach (setting the weighting functions equal to the basis functions), a discrete form of Eq. (2) is obtained for each tetrahedron [9]:

(6)

where

. (7)

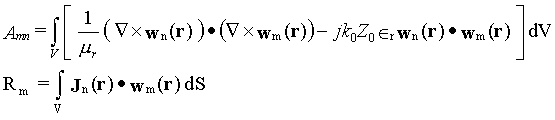
For the calculation of the terms in the above equation, refer to appendices A, B in [9].

The above equation can be obtained for all the tetrahedra in the volume of interest. All these individual equations are then combined into a global equation.

(8)

Some of the values in the E vector are known (forced). Therefore the above equation can be partitioned into forced edges and unknown edges as follows,

. (9)

 

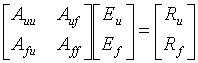
The unknown field elements can be found by using:

. (10)