The dielectric cube in Figure 16 has a length of 0.2l on one side, where l is the wavelength in free space. It is illuminated by an incident plane wave, which travels along the +z axis. The E field is polarized along the x axis with a magnitude of 1 volt/meter. This example was previously analyzed by T. K. Sarkar et al.[1], B. J. Rubin and S. Dajiavad [2].

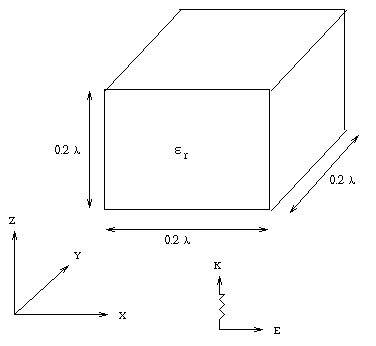
First, the relative permittivity of the cube is set to 1-j1000. The frequency of the plane wave is assumed to be 600 MHz. Thus, the length of each side of the cube is 10 centimeters. The input file for SIFT5 is as follows,

Figure 16. A dielectric cube illuminated by a plane wave.

# example 4: a dielectric cube (er = 1-j1000 ) illuminated by a plane wave

unit 1 mm

boundary -50 -50 -50 50 50 50

celldim -50 50 25 x

celldim -50 50 25 y

celldim -50 50 25 z

dielectric -50 -50 -50 50 50 50 1.0 -1000.0

eplane 600 90 0 0 0 1.0

default_out example4.out

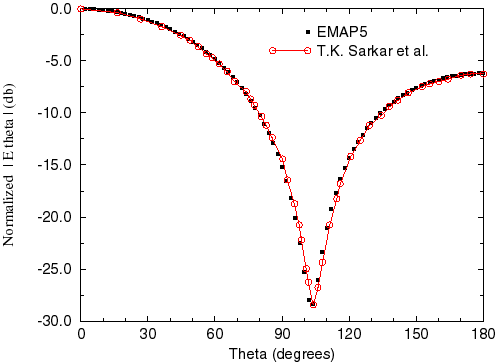
The dielectric cube is divided into 64 bricks, then 320 tetrahedra. In Figure 17, the normalized far field obtained by EMAP5 is compared to those calculated in [1][2].

Second, the dielectric constant of the cube is set to 9.0. The "dielectric" line in the input file for SIFT5 needs to be changed as follows,
dielectric -50 -50 -50 50 50 50 9.0 0.0

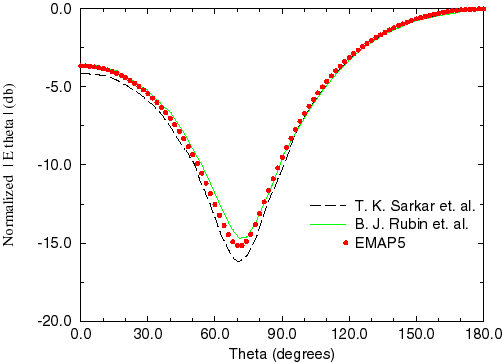
In Figure 18, the normalized far field obtained by EMAP5 is compared to those calculated in [1][2]. In both cases, the results obtains by EMAP5 agree with the references.

Figure 17. Comparison of far field E_q when e r = 1-j1000.

 

Figure 18. Comparison of far field E_q when er =9.