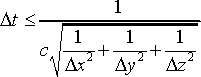The Finite Integration TechniqueThe Finite Integration Technique (FIT) is a consistent formulation for the discrete representation of Maxwell's equations on spatial grids. First proposed by Weiland [1] in 1977, the finite integration technique can be viewed as a generalization of the FDTD method. It is also similar to the finite element method. Weiland [1, 2] proposed exact algebraic analogues to Maxwell's equations that guarantee physical properties of computed fields and lead to a unique solution. By discretizing the integral form of Maxwell's equations on a pair of dual interlaced discretization grids, the finite integration technique generates so-called Maxwell's Grid Equations (MGEs) that guarantee the physical properties of computed fields and lead to a unique solution.
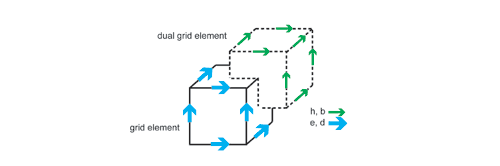
where e is the electric voltage between the grid points and h is the magnetic voltage between dual grid points. d, b and j are fluxes over grid or dual grid faces. The allocation of the voltage and flux components on the dual grids is shown in Figure 3.
Figure 3: Allocation of the voltage and flux components in the mesh. Due to the consistent transformation, the analytical
properties of the fields are maintained resulting in corresponding discrete
topological operators on the staggered grid duplet. The topology matrices
After discretization, the material property relations become
where Mε, Mμ and Mk are matrices describing the material properties. The relations in (1) - (4) are exact on a given mesh, however, the material matrices contain the unavoidable approximations of any numerical procedure. In addition, these matrices have diagonal form [78]. Employing a so-called leap-frog scheme which samples values of e and h at times separated by a half time step, the MGEs can be rewritten as a set of two recursion formulas:
The recursion is stable if the time step inside an equidistant grid is restricted by the Courant criterion to
The calculation of each further time step only requires one matrix-vector multiplication. Thus it has the advantage being an explicit algorithm. The FIT can be applied to different mesh types [3, 4]. On Cartesian grids, the time-domain FIT is equivalent to FDTD. References[1] T. Weiland, "A discretization method for the solution of Maxwell's equations for six-component fields", Electronics and Communication (AEÜ), vol. 31, p. 116, 1977. [2] T. Weiland, "Time domain electromagnetic field computation with finite difference methods", International Journal of Numerical Modelling, vol. 9, pp. 295-319, 1996. [3] B. Krietenstein, R. Schuhmann, P. Thoma, and T. Weiland, "The perfect boundary approximation technique facing the challenge of high precision field computation", in Proceedings of the XIX International Linear Accelerator Conference (LINAC'98), Chicago, USA, 1998, pp. 860-862. [4] M. Walter, I. Munteanu, "FIT for EMC," Proc. of the 17th International Zurich Symposium on Electromagnetic Compatibility, 2006, pp. 15-17. |
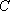 ,
,
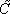 ,
,
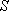 and
and
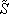 correspond to the curl- and the div-
operators. The tilde means that the operator is performed on the dual grid.
correspond to the curl- and the div-
operators. The tilde means that the operator is performed on the dual grid.