Operator theoretic methods for data-driven analysis and control of dynamical systems
Operator theoretic methods for data-driven analysis and control of dynamical systems
Duality in stability and control from linear operator perspective:
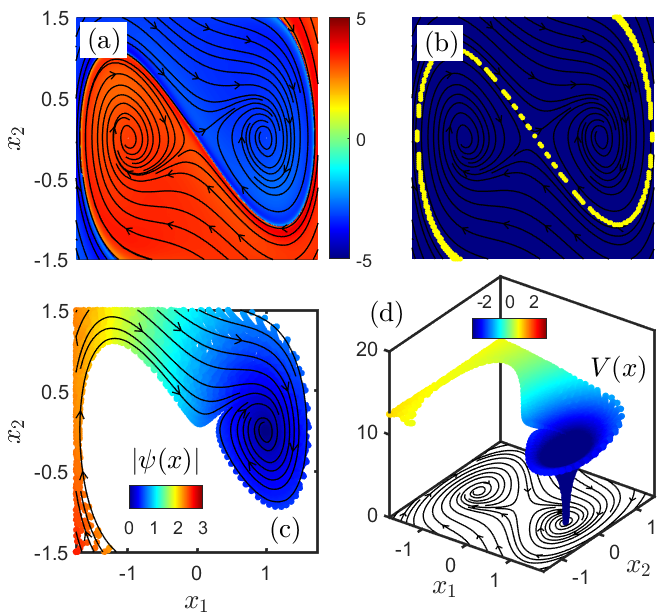
We have introduced novel operator theoretical methods for stability analysis and optimal control design for dynamical systems. The transformative idea we proposed is to shift the focus from the point-wise nonlinear evolution of dynamical systems on the finite-dimensional state space to ensemble linear evolution of functions on infinite dimensional space. With every nonlinear dynamical system, one can associate two linear operators called Perron-Frobenius (P-F) and Koopman operators.
Spectral Koopman methods for analysis and control:
The proposed research aims to discover methods based on the spectral analysis of the Koopman operator for the data-driven analysis and synthesis of nonlinear systems. The Koopman operator provides for a linear lifting of the nonlinear system dynamics in the function space.
Read More
We have introduced novel operator theoretical methods for stability analysis and optimal control design for dynamical systems. The transformative idea we proposed is to shift the focus from the point-wise nonlinear evolution of dynamical systems on the finite-dimensional state space to ensemble linear evolution of functions on infinite dimensional space. With every nonlinear dynamical system, one can associate two linear operators called Perron-Frobenius (P-F) and Koopman operators.
Spectral Koopman methods for analysis and control:
The proposed research aims to discover methods based on the spectral analysis of the Koopman operator for the data-driven analysis and synthesis of nonlinear systems. The Koopman operator provides for a linear lifting of the nonlinear system dynamics in the function space.
Cyber-Physical Systems
Cyber-Physical Systems
Fundamental limitations for control of dynamical systems over networks:
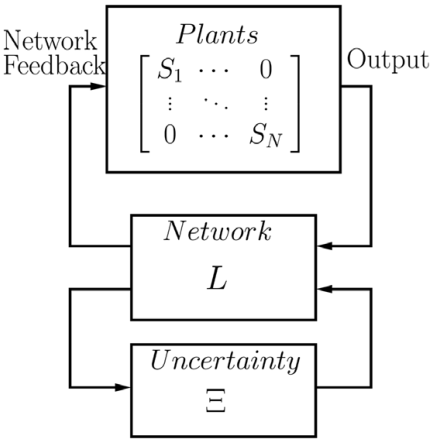
We have discovered a systematic framework for analyzing and designing network-controlled systems in the presence of uncertainty. This includes discovering fundamental limitation results for estimating and stabilizing nonlinear systems over uncertain communication channels. This research mainly connected fundamental limitations for nonlinear stabilization and estimation with the measure-theoretic entropy of steady-state invariant measure of the open loop system.
Control and optimization over uncertainty networks:
The main contribution of this work is to understand fundamental tradeoffs that arise in the control of linear and nonlinear dynamical systems over networks in the presence of uncertainty. For systems with linear dynamics, we have provided a systematic convex optimization-based approach for synthesizing control robust to stochastic network communication uncertainty.
Read More
We have discovered a systematic framework for analyzing and designing network-controlled systems in the presence of uncertainty. This includes discovering fundamental limitation results for estimating and stabilizing nonlinear systems over uncertain communication channels. This research mainly connected fundamental limitations for nonlinear stabilization and estimation with the measure-theoretic entropy of steady-state invariant measure of the open loop system.
Control and optimization over uncertainty networks:
The main contribution of this work is to understand fundamental tradeoffs that arise in the control of linear and nonlinear dynamical systems over networks in the presence of uncertainty. For systems with linear dynamics, we have provided a systematic convex optimization-based approach for synthesizing control robust to stochastic network communication uncertainty.
Information Flow and Control Over Networks
Information Flow and Control Over Networks
Information-based causality measure in a dynamical system:
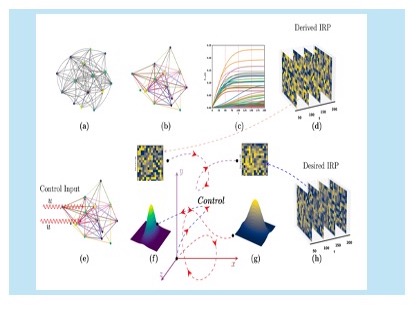
Information flow and causality are the most fundamental concepts for analyzing and designing various engineering and natural sciences systems. A mathematically precise definition of information flow developed with dynamics in mind is necessary for the rigorous formulation of autonomy in a network dynamical system.
Control of information flow over networks:
Information flow among nodes in a complex network describes the overall cause-effect relationships among the nodes. It provides a better understanding of the contributions of these nodes, individually or collectively, towards the underlying network dynamics. Variations in network topologies result in varying information flows among nodes.
Read More
Information flow and causality are the most fundamental concepts for analyzing and designing various engineering and natural sciences systems. A mathematically precise definition of information flow developed with dynamics in mind is necessary for the rigorous formulation of autonomy in a network dynamical system.
Control of information flow over networks:
Information flow among nodes in a complex network describes the overall cause-effect relationships among the nodes. It provides a better understanding of the contributions of these nodes, individually or collectively, towards the underlying network dynamics. Variations in network topologies result in varying information flows among nodes.

Off-road Autonomy and Robotics
Off-road Autonomy and Robotics
This research focuses on developing a systematic data-driven analytical and computational framework for the navigation of autonomous vehicles in the off-road environment. The data-driven tools are based on linear operator theory involving Koopman and Perron-Frobenius operators. The developed framework is tested on an experimental platform consisting of an F1TENTH vehicle, 1/5th scale Hunter SE. We are currently implementing the framework for full-scale Warthog and MRZR vehicles.

Network Power System
Network Power System
In applications involving network power systems, our research work is focused on a couple of different problems, which include real-time stability monitoring, stochastic stability and performance analysis of power systems in the presence of uncertain renewable, robust distributed optimization of a distributed system, data-driven analytics involving linear operator theoretic methods for reduced order modeling, and cyber security of power grid. We have discovered data-driven methods based on the dynamical system theory for the real-time rotor angle and power system voltage stability monitoring using time-series data from Phasor Measurement Units (PMUs).
