Absolute points

A surprising property of conics is that every circle intersects the ideal line, W=0, at two fixed points. To see this, note that a circle is a conic with all off-diagonal elements (c₁₂, c₁₃, and c₂₃) set to zero and all diagonal elements equal:

X² + Y² + W² = 0,

which therefore intersects the ideal line W=0 at

X² + Y² = 0.

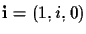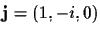This equation has two complex roots, known as the absolute points: $\ensuremath{{\bf i}} = (1, i, 0)$ and $\ensuremath{{\bf j}} = (1, -i, 0)$. (Although we have, for simplicity, assumed that homogeneous coordinates are real, they can in general be the elements of any commutative field in which 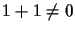$1+1 \ne 0$ [1, p. 112].) It will be shown in the next two subsections that the absolute points remain invariant under similarity transformations, which makes them useful for determining the angle between two lines.