

Next: Intersections and unions of
Up: Projective Space
Previous: Projective Space
Recall from the Section 2 that the
coordinates of the line passing through two points
 and
and
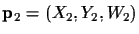 is given by
is given by
Notice that these three coordinates are just the determinants of the
three
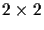 submatrices of the following matrix:
submatrices of the following matrix:
taken in the appropriate order and given the appropriate sign.
The procedure is similar in
 .
The coordinates of the
line
.
The coordinates of the
line
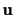 passing through two points
passing through two points
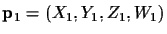 and
and
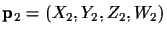 is given by
the determinants of the six
is given by
the determinants of the six
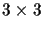 submatrices of the following matrix:
submatrices of the following matrix:
In other words,
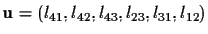 ,
where
,
where
These coordinates lij are called the Plücker
coordinates of the line. It is fairly easy to show that,
if the points
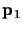 and
and
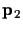 are not ideal
(that is, W1 and W2 are not zero),
then the coordinates have a nice Euclidean interpretation:
are not ideal
(that is, W1 and W2 are not zero),
then the coordinates have a nice Euclidean interpretation:
where
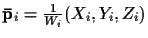 ,
i=1,2,
are the coordinates of the corresponding Euclidean
points. That is, the first three Plücker
coordinates describe the direction of the line, and the last
three coordinates describe the plane containing the line and the
origin and the distance from the origin to the line. Therefore the
six Plücker coordinates are sufficient to describe the
line. The coordinates are not independent, however, because they
always satisfy
,
i=1,2,
are the coordinates of the corresponding Euclidean
points. That is, the first three Plücker
coordinates describe the direction of the line, and the last
three coordinates describe the plane containing the line and the
origin and the distance from the origin to the line. Therefore the
six Plücker coordinates are sufficient to describe the
line. The coordinates are not independent, however, because they
always satisfy
l41l23+l42l31+l43l12=0,
which can be derived by noting that the
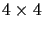 determinant
determinant
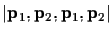 is identically zero.
is identically zero.
Where does the magic number six come from? That is, why do we need
six parameters to represent a line in
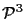 ? Interestingly, it turns
out that it takes
(n+1k) parameters
to represent an
entity defined by k points in a space requiring n+1 parameters for
each point (To see this, count the number of submatrices in the
matrix above).
For example, in
? Interestingly, it turns
out that it takes
(n+1k) parameters
to represent an
entity defined by k points in a space requiring n+1 parameters for
each point (To see this, count the number of submatrices in the
matrix above).
For example, in
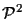 a point requires
(31) = 3 parameters, and a line (which is defined by
two points) also requires
(32) = 3 parameters. In
a point requires
(31) = 3 parameters, and a line (which is defined by
two points) also requires
(32) = 3 parameters. In
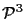 ,
a point requires
(41) = 4 parameters, a line
(42) = 6 parameters, and a plane
(43) = 4 parameters.
,
a point requires
(41) = 4 parameters, a line
(42) = 6 parameters, and a plane
(43) = 4 parameters.


Next: Intersections and unions of
Up: Projective Space
Previous: Projective Space
Stanley Birchfield
1998-04-23
![]() and
and
![]() is given by
is given by
![\begin{displaymath}\left[\matrix{\ensuremath{{\bf p}} _1 & \ensuremath{{\bf p}} ...
...
\left[\matrix{X_1 & X_2 \cr Y_1 & Y_2 \cr W_1 & W_2}\right],
\end{displaymath}](img114.gif)
![]() .
The coordinates of the
line
.
The coordinates of the
line
![]() passing through two points
passing through two points
![]() and
and
![]() is given by
the determinants of the six
is given by
the determinants of the six
![]() submatrices of the following matrix:
submatrices of the following matrix:
![\begin{displaymath}\left[\matrix{\ensuremath{{\bf p}} _1 & \ensuremath{{\bf p}} ...
...x{X_1 & X_2 \cr Y_1 & Y_2 \cr Z_1 & Z_2 \cr W_1 & W_2}\right].
\end{displaymath}](img117.gif)
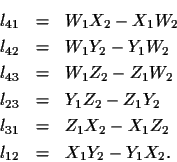
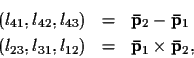
![]() ? Interestingly, it turns
out that it takes
(n+1k) parameters
to represent an
entity defined by k points in a space requiring n+1 parameters for
each point (To see this, count the number of submatrices in the
matrix above).
For example, in
? Interestingly, it turns
out that it takes
(n+1k) parameters
to represent an
entity defined by k points in a space requiring n+1 parameters for
each point (To see this, count the number of submatrices in the
matrix above).
For example, in
![]() a point requires
(31) = 3 parameters, and a line (which is defined by
two points) also requires
(32) = 3 parameters. In
a point requires
(31) = 3 parameters, and a line (which is defined by
two points) also requires
(32) = 3 parameters. In
![]() ,
a point requires
(41) = 4 parameters, a line
(42) = 6 parameters, and a plane
(43) = 4 parameters.
,
a point requires
(41) = 4 parameters, a line
(42) = 6 parameters, and a plane
(43) = 4 parameters.