Previous:PMLs
Next: Summary
Contents

---

VIII. SPARSE MATRIX METHODS

A. STORAGE OF SPARSE MATRICES

    The finite element method (FEM) has a lot of advantages. One of the main advantages is that the final matrix generated is sparse. This makes FEM very attractive to users who are concerned with memory conservation. Typically the number of non-zero elements in a row is very small compared to the number of rows and therefore storing all the elements is not efficient. One method for storing sparse matrices is the row-indexed storage method [14] and this has been implemented in EMAP-4. This method of storage makes it easy for the matrix to be constructed. It also makes the use of iterative methods like the Complex Biconjugate method (CGBG) easy. The CBCG employs a lot of matrix-vector multiplications, which this kind of storage easily supports.

    The row-indexed storage method uses three matrices to store the non-zero elements of a sparse matrix. Let the number of rows be N. The first matrix is an N ´ 1 vector and stores the number of non-zero elements in each row. This is called the Index matrix. This matrix consists of integers and takes up very little memory. The second matrix is an N ´ M matrix. Here M is the maximum number of non-zero elements in any row. This stores the non-zero elements in each row and is called the Data matrix. Typically all the rows have nearly the same number of non-zero elements and therefore the number of elements in this matrix is very close to the actual number of non-zero elements. The third matrix is of the same size as the second matrix. This matrix is called ColNos and stores the column number corresponding to the entries in the Data matrix.

    This method of storing matrices is illustrated by a simple example. Consider the matrix shown below. It is fairly sparse.

(25)

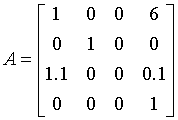
    The corresponding storage matrices are

(26)

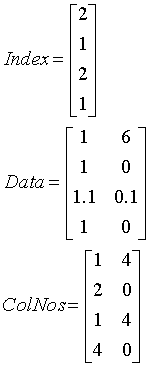
    The next section describes the Complex Biconjugate Gradient method, which uses the sparsity of the FEM matrix to solve the final equation.

B.THE COMPLEX BI-CONJUGATE GRADIENT METHOD

    The Complex Biconjugate Gradient method (CBCG) is used to solve the final complex matrix equation. The CBCG is an iterative method and requires only matrix-vector multiplications. It is more effective for solving sparse matrix equations than the LU decomposition method in both memory requirements and solution time.

    The CBCG method was first introduced by D.A.H. Jacobs [7]. A brief description of the algorithm is given below:
Consider a complex matrix equation as follows;

[A][X]=[b] (27)
where [A] is an N´ N complex matrix, and [b] and [X] are N complex column vectors. Both [A] and [b] are known while [X] is unknown. In the CBCG, four column vectors are defined as follows:

1. the residue r
2. the bi-residue r bar
3. the direction vectorp
4. the bi-direction vectorp bar

These vectors are initialized as:

(28)

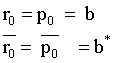
where * denotes the complex conjugate.

The inner product of two complex column vectors is defined as follows,

<p₁, p₂> º (p₁*)^T p_2. (29)

The following steps are repeated N times at most. For k=0, … , N-1;

calculate the step-length parameter;

. (30)

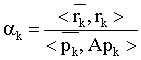
The new solution estimate then becomes,

. (31)

The new residue and bi-residue are calculated as follows,

. (32)

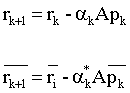
The bi-conjugacy coefficient is calculated using the following formula,

. (33)

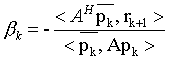
The Hermitian of A is defined as,

A^{H º} (A*)^T (34)

where T denotes transpose.

The new direction and bi-direction vectors are given by,

. (35)

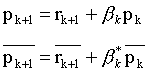
This iteration is continued until a termination condition is satisfied:

(36)

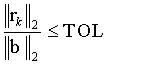
where TOL is a number defining the tolerance. The value of TOL depends on the application. Typically, TOL = 1´ 10^-5 is sufficient. EMAP4 uses a default value of 1´ 10^-5 for TOL. The value of TOL can be modified by changing the macro TOLERANCE in the source code.

    Although the CBCG solver conserves memory, it is an iterative method that may have difficulty converging in some situations, for example in situations where the matrix is ill-conditioned. In general, the value of the tolerance dictates the number of significant digits in the answer. For the problems modeled in this thesis, the errors due to meshing usually make it unnecessary to have a tolerance less than 1´ 10^-4. The round-off error of double precision is 2.22´ 10^-16. If double precision is used for the matrix calculations, round-off errors will not reduce the effectiveness of CBCG considerably. In EMAP4, all data is stored in double precision.