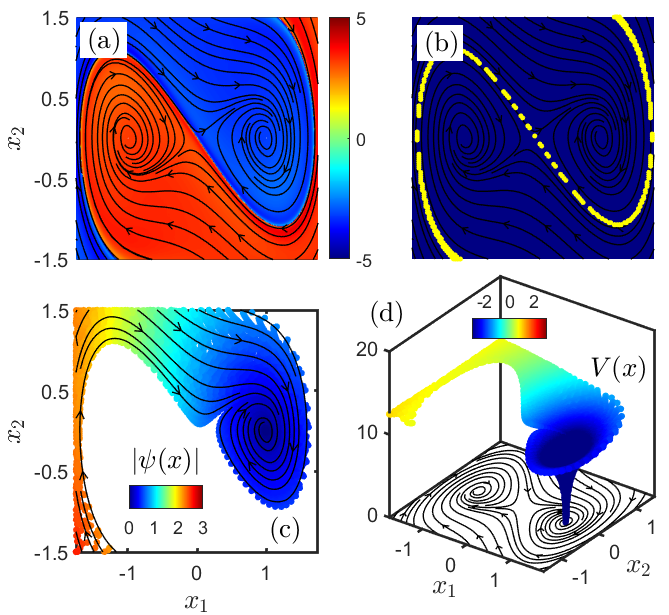
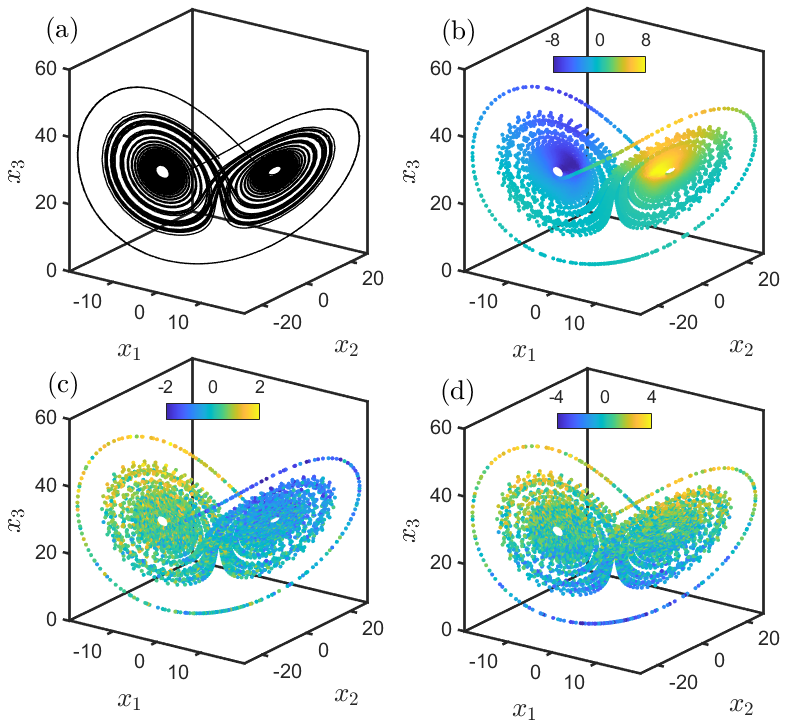
The proposed research aims to discover methods based on the spectral analysis of the Koopman operator for the data-driven analysis and synthesis of nonlinear systems. The Koopman is a linear operator and provides for a linear lifting of the nonlinear system dynamics in the function space. The eigenfunctions of the Koopman operator can be used as coordinates to transform the nonlinear dynamics into a linear system. The eigenfunctions of the Koopman operator also carry information about the underlying state space geometry. In particular, the stable and unstable manifolds of the nonlinear system can be obtained as zero-level curves of the Koopman eigenfunctions. This connection between the Koopman eigenfunctions and the state space geometry is exploited to analyze and synthesize nonlinear control systems. In our current research, we are developing spectral Koopman methods for reachability analysis, safe control design, uncertainty propagation, and optimal control design.

The approximation of the Koopman operator and its spectrum can be computed from the data without knowing system dynamics. Hence, the use of Koopman theory provides a natural pathway for developing systematic data-driven analysis and synthesis methods for nonlinear control systems. In our current research, we are exploiting various approaches, including Deep-Network-Networks, Reproducing Kernel Hilbert Space (RKHS), and techniques inspired by statistical mechanics for approximation of the Koopman spectrum.

[1] Umesh Vaidya, When Koopman Meets Hamilton and Jacobi, Preprint.

[2] Umesh Vaidya, Spectral Theory of Koopman Operator and Nonlinear Optimal Control, IEEE CDC, 2022.

Convex Approach to Data-driven Control and Safety

---

It is well known that the codesign problem of finding a controller and Lyapunov function is non-convex. The control problem can be alternately formulated in the dual space of densities, where the density function of the Lyapunov measure is used for verifying the weaker notion of almost everywhere stability. The codesign problem for jointly finding the Lyapunov measure and controller is convex. The convex framework for stabilizing controller design can be extended for the optimal control design. The duality in stability theory and optimal control design can be naturally viewed through the lenses of linear transfer operator theory involving Perron-Frobenius and Koopman operators. The Lyapunov function or the Hamilton Jacobi equation can be associated with the linear Koopman operator, and the Lyapunov density or Lyapunov measure is related to the Perron-Frobenius operator.

The main advantage of presenting the convex framework for optimal control design using a linear transfer operator is that the data-driven methods developed for the finite-dimensional approximation of the linear operators can be used for the data-driven approximation of the optimal controller. The data-driven aspect of the linear operator theory combined with the convex formulation of the optimal control problem presents a powerful approach for data-driven nonlinear control.

[1] Umesh Vaidya and Duvan Tellez Castro, Data-driven stochastic optimal control with safety constraints using linear transfer operator, IEEE Transactions on Automatic Control.

[2] Moyalan, Joseph, Hyungjin Choi, Yongxin Chen, and Umesh Vaidya. “Data-driven optimal control via linear transfer operators: A convex approach.” Automatica 150 (2023): 110841.

[3] Moyalan, Joseph, Yongxin Chen, and Umesh Vaidya. “Convex Approach to Data-Driven Off-Road Navigation via Linear Transfer Operators.” IEEE Robotics and Automation Letters 8, no. 6 (2023): 3278-3285.

[4] Huang, Bowen, and Umesh Vaidya. “A Convex Approach to Data-Driven Optimal Control via Perron–Frobenius and Koopman Operators.” IEEE Transactions on Automatic Control 67, no. 9 (2022): 4778-4785.

Application to Vehicle Autonomy and Robotic Systems

---

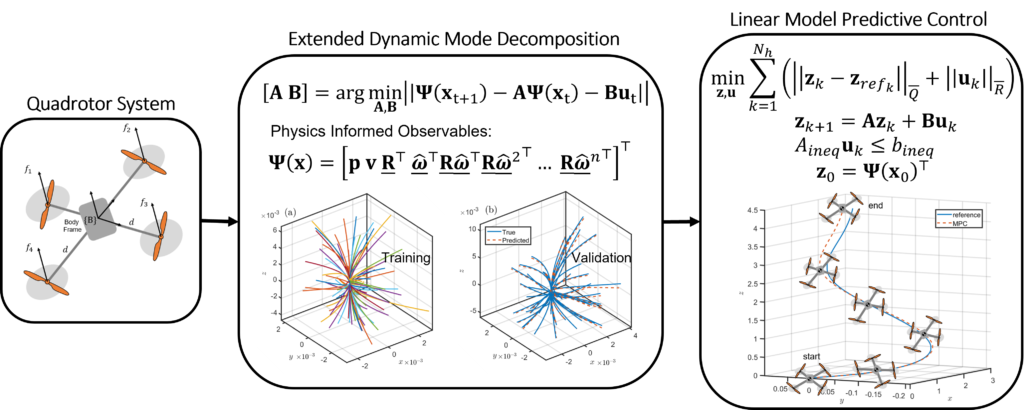
The focus of this research work is on the application of linear operator theory for the robotic system. We are working on two robotics platforms in this application: a quadruped robot and an autonomous vehicle. In these applications, we are developing data-driven and model-based methods for the control and safe operations of robotic systems. One of the main contributions is the development of Koopman-based model predictive control (MPC) for controlling autonomous F1TENTH vehicles and quadrotors. For the control of the F1TENTH vehicle and Unitree Go1 quadruped robot, we are using experimental data obtained under different operating conditions to generate Koopman linear control model for the design of MPC control. Furthermore, this MPC control is combined with navigation density-based safety certificates to design safe and optimal control strategies.

In our research, we have overcome the fundamental problem associated with the navigation function by providing analytical construction of the navigation density function used for navigating with safety constraints. The proposed construction of navigation density allows us to navigate in an environment consisting of dynamic obstacles and a dynamically changing target set. Therefore, the navigation density can be viewed as dual to the navigation function. In contrast to the navigation function, the navigation density takes an infinite value at the target set and is zero on the obstacle set.

Furthermore, we have applied the navigation density to the quadruped planning problem. In this work, we apply the feedback control onto the legged locomotion problem, resulting in safe navigation.

Some of our current aim is to approach this density navigation problem for unstructured terrains. Our current progress in this area can be seen in the video below:

[1] Andrew Zheng, Sriram S.K.S Narayanan, and Umesh Vaidya, Analytical Construction of Density Functions for Navigation with Safety Constraints, Submitted for publication in journal.

Application to Network Power Systems

---

For the power system application, we are exploring variety of problems of practical interest to power system operator including providing methods for computing critical clearing time, optimal operation of battery resources for profit maximization, grid welfare, determining optimal location and sizing of battery resources, and transient stability assessment in the presence of renewable uncertainty.