Transient Acoustic Scattering using Adaptive Discontinuous Galerkin Finite Element Method

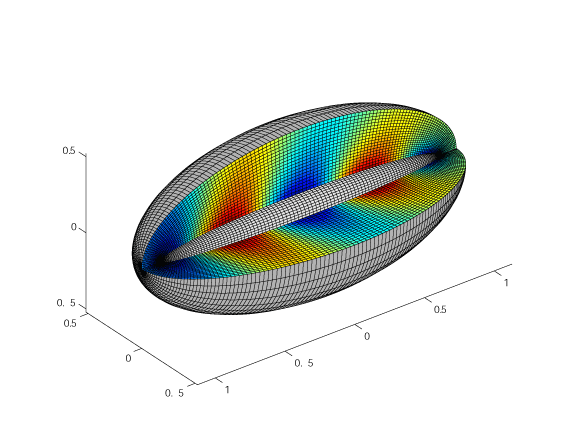
Adaptive Discontinuous Galerkin Finite Element Method (DGFEM) scattered field solution from an ellipse in an unbounded region with corresponding adaptive mesh at snapshots in time. Waves are allowed to pass through the circular nonreflecting boundary, using the sequence of high-order accurate radiation conditions given in (L.L. Thompson, R. Huan, D. He, `Accurate radiation boundary conditions for the two-dimensional wave equation on unbounded domains,’ Comput. Methods in Appl. Mech. Engrg, 191, 311-351, 2001). Initially, the scattered field is localized near the surface of the scatterer and then expands as the pulse progresses past an elliptic scatterer. As the wave propagates throughout the grid, elements are refined near wavefronts and unrefined where the solution is smooth or quiescent. This provides efficient real-time wave tracking over large distances and time.

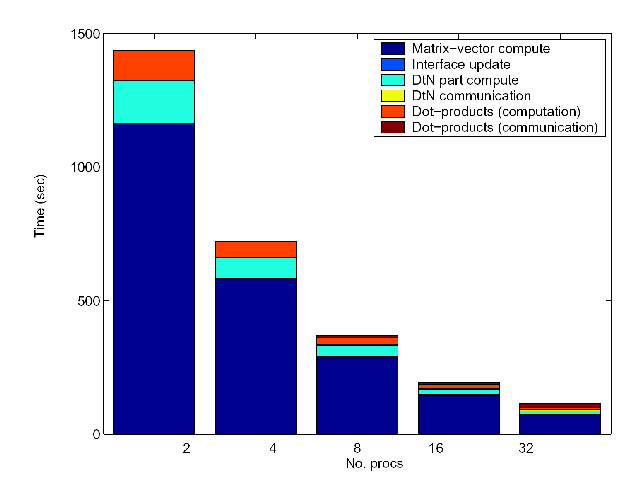
Parallel Iterative Solution for Three-Dimensional Acoustic Scattering