

Next: Acknowledgment
Up: An Introduction to Projective
Previous: Vanishing points
Let
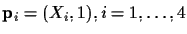 be
four points on the projective line. (In this demonstration, we will only consider
finite points, although the cross ratio holds for infinite points as well.)
Define the distance
be
four points on the projective line. (In this demonstration, we will only consider
finite points, although the cross ratio holds for infinite points as well.)
Define the distance
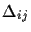 between two points i and j as
between two points i and j as
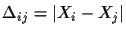 .
What we want to show is that the cross ratio
.
What we want to show is that the cross ratio
is preserved under projective projection of the points.
A point
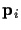 is projected through a
is projected through a
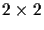 transformation matrix T to
a new point
transformation matrix T to
a new point
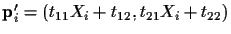 .
Therefore, the new coordinate
.
Therefore, the new coordinate
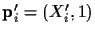 is defined by:
is defined by:
Then, the distance between two points X'i and X'j is
where
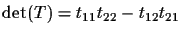 .
The ratio between two
distances, one from a point X'i to another point X'j, and another
from the same point X'i to a third point X'k, is
.
The ratio between two
distances, one from a point X'i to another point X'j, and another
from the same point X'i to a third point X'k, is
which is the original ratio
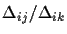 ,
multiplied by a
constant that is dependent only upon the coordinates Xj and Xk.
A similar ratio
,
multiplied by a
constant that is dependent only upon the coordinates Xj and Xk.
A similar ratio
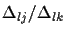 ,
taken with respect to another
point Xl, has this same constant, and therefore dividing the two
ratios causes the constants to cancel:
,
taken with respect to another
point Xl, has this same constant, and therefore dividing the two
ratios causes the constants to cancel:
showing that the cross ratio is unaffected by projection.
Suppose that one of the points, say
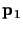 ,
is at infinity (i.e., its
second coordinate is zero).
Then, dividing by the second coordinate (which is what we normally do
to transform the point into the required form) yields
,
is at infinity (i.e., its
second coordinate is zero).
Then, dividing by the second coordinate (which is what we normally do
to transform the point into the required form) yields
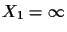 .
Substituting into the above formula yields:
.
Substituting into the above formula yields:
since the terms with 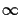 cancel each other. (Technically speaking,
we must take the limit of the equation as X1 tends to
cancel each other. (Technically speaking,
we must take the limit of the equation as X1 tends to 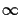 ,
but
the result is the same.) Similarly, if any of the other points are at
infinity, we simply cancel the terms containing the point, and the result is
the cross ratio. Remember that at most one point may be at infinity, because
the points must be distinct, and there is only one point at infinity on
the projective line.
,
but
the result is the same.) Similarly, if any of the other points are at
infinity, we simply cancel the terms containing the point, and the result is
the cross ratio. Remember that at most one point may be at infinity, because
the points must be distinct, and there is only one point at infinity on
the projective line.


Next: Acknowledgment
Up: An Introduction to Projective
Previous: Vanishing points
Stanley Birchfield
1998-04-23
![]() be
four points on the projective line. (In this demonstration, we will only consider
finite points, although the cross ratio holds for infinite points as well.)
Define the distance
be
four points on the projective line. (In this demonstration, we will only consider
finite points, although the cross ratio holds for infinite points as well.)
Define the distance
![]() between two points i and j as
between two points i and j as
![]() .
What we want to show is that the cross ratio
.
What we want to show is that the cross ratio
![]() is projected through a
is projected through a
![]() transformation matrix T to
a new point
transformation matrix T to
a new point
![]() .
Therefore, the new coordinate
.
Therefore, the new coordinate
![]() is defined by:
is defined by:
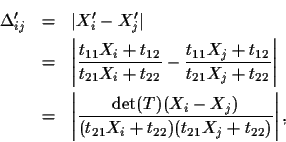
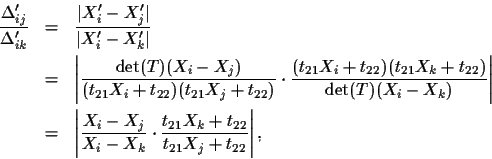
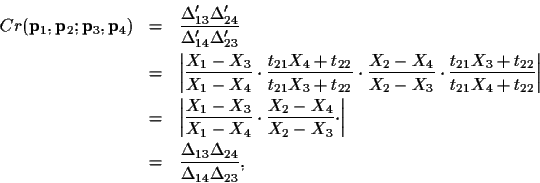
![]() ,
is at infinity (i.e., its
second coordinate is zero).
Then, dividing by the second coordinate (which is what we normally do
to transform the point into the required form) yields
,
is at infinity (i.e., its
second coordinate is zero).
Then, dividing by the second coordinate (which is what we normally do
to transform the point into the required form) yields
![]() .
Substituting into the above formula yields:
.
Substituting into the above formula yields: