Vanishing points

Anyone who has taken a course in perspective drawing is familiar with the notion that lines on the paper which represent parallel lines in the world intersect on the paper at a point known as the vanishing point. Each set of lines has a different vanishing point. But, just what is a vanishing point? Projective geometry sheds light on this issue.

Because image formation is the projection from a 3D world to a 2D surface, each point on the image plane is the projection of an infinite number of points in the world. Usually, the closest point is opaque and therefore we think of the point on the image plane as being the projection of only one point in the world. However, ideal points in the world (i.e., ideal points in 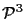), always project onto the image plane regardless of the opacity of other points. Each point on the image plane is the projection of an ideal point. To see this, consider the following perspective projection equation (a general projective transformation is used for simplicity) from an ideal point [X,Y,Z,0]^T in the world to a point [x,y,w]^T in the image plane:

$$\left[\matrix{x \cr y \cr w} \right] = \left[\matrix{t_{11} &... ...}& t_{34} }\right] \left[\matrix{X \cr Y \cr Z \cr 0} \right].$$

Because the matrix is full rank, each ideal point projects to a different point on the image plane. Since parallel lines in 3D space intersect at an ideal point in 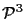, their projections in the image plane must still intersect at a point. But now, through the projection matrix, the ideal point has become a ``real'' point, in the sense that it is no longer ideal. However, some ideal points do not become ``real'' points. If the ideal point represents a direction that is parallel to the image plane, then the dot product of the ideal point with the third row of the matrix (which is the z axis of the plane) is zero, and the projected point is still ideal. 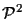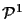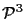Just as the ideal points of have a one-to-one correspondence with all the points in , so the ideal points of have a one-to-one correspondence with all the points in 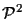. Thus, we see that the fact that parallel lines in the world intersect when drawn on a piece of paper follows naturally from projective geometry.