A collineation of
![]() is defined as a mapping from the plane to
itself such that the collinearity of any set of points is preserved. Such a
mapping can be achieved with matrix multiplication by a
is defined as a mapping from the plane to
itself such that the collinearity of any set of points is preserved. Such a
mapping can be achieved with matrix multiplication by a
![]() matrix
T. Each point
matrix
T. Each point
![]() is transformed into a point
is transformed into a point
![]() :
:
To transform a line
![]() into a line
into a line
![]() ,
we note that collinearity must
be preserved, that is, if a point
,
we note that collinearity must
be preserved, that is, if a point
![]() lies on the line
lies on the line
![]() ,
then the
corresponding point
,
then the
corresponding point
![]() must lie on the corresponding line
must lie on the corresponding line
![]() .
Therefore,
.
Therefore,
From these results, it is not hard to show that a point conic C transforms to T-TCT-1, and a line conic |C|C-1 transforms to T|C|C-1TT.
Regarding transformations, recall that projective ![]() affine
affine ![]() similarity
similarity ![]() Euclidean.
Let's study the matrix T to uncover the relationships between these
various geometries. First we will write out the elements of T, for
reference:
Euclidean.
Let's study the matrix T to uncover the relationships between these
various geometries. First we will write out the elements of T, for
reference:
![\begin{displaymath}T_{projective} = \left[\matrix{t_{11} & t_{12} & t_{13} \cr
t_{21} & t_{22} & t_{23} \cr
t_{31} & t_{32} & t_{33}}\right].
\end{displaymath}](img71.gif)
The affine plane is just the projective plane minus the ideal line.
Therefore, affine transformations must preserve the ideal line and
the ideal points,
that is, any point
[X, Y, 0]T must be transformed into
![]() for some arbitrary scaling
for some arbitrary scaling
![]() :
:
![\begin{displaymath}\ensuremath{\alpha}\left[\matrix{X \cr Y \cr 0}\right] = T
\left[\matrix{X \cr Y \cr 0}\right],
\end{displaymath}](img74.gif)
![\begin{displaymath}T_{af\!fine} = \left[\matrix{t_{11} & t_{12} & t_{13} \cr
t_{21} & t_{22} & t_{23} \cr
0 & 0 & t_{33}}\right],
\end{displaymath}](img75.gif)
Unlike affine transformations,
similarity transformations preserve angles and ratios of lengths.
Delaying the derivation for a moment, we simply state the result:
Under Euclidean transformation, scale is important, and therefore the
point
![]() must first be converted to Euclidean coordinates by
dividing by its third element. The transformation then is
must first be converted to Euclidean coordinates by
dividing by its third element. The transformation then is
In closing this section, we offer one final proposition, along with its proof:
The ``only if'' is rather easy to see: The absolute point
![]() is transformed through equation (3) to
the point
is transformed through equation (3) to
the point
![]() ,
which is equivalent because the scale
factor is ignored.
,
which is equivalent because the scale
factor is ignored.
The ``if'' is a little more complicated, but still rather straightforward.
Starting with the unrestricted equation for T,
![\begin{displaymath}T = \left[\matrix{t_{11} & t_{12} & t_{13} \cr
t_{21} & t_{22} & t_{23} \cr
t_{31} & t_{32} & t_{33}}\right],
\end{displaymath}](img82.gif)
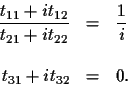
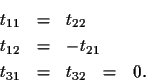
![\begin{displaymath}T = \left[\matrix{t_{11} & t_{12} & t_{13} \cr
-t_{12} & t_{11} & t_{23} \cr
0 & 0 & t_{33}}\right].
\end{displaymath}](img85.gif)
![\begin{displaymath}T = \left[\matrix{\cos \theta & \sin \theta & t_{13}/k \cr
-...
...\theta & \cos \theta & t_{23}/k \cr
0 & 0 & t_{33}/k}\right],
\end{displaymath}](img88.gif)