The cross ratio

As mentioned before, projective geometry preserves neither distances nor ratios of distances. However, the cross ratio, which is a ratio of ratios of distances, is preserved and is therefore a useful concept. Given four collinear points $\ensuremath{{\bf p}_{1}}$, $\ensuremath{{\bf p}_{2}}$, $\ensuremath{{\bf p}_{3}}$, and $\ensuremath{{\bf p}_{4}}$ in , denote the Euclidean distance between two points $\ensuremath{{\bf p}_{i}}$ and $\ensuremath{{\bf p}_{j}}$ as $\Delta_{ij}$. Then, one definition of the cross ratio is the following:

$$Cr(\ensuremath{{\bf p}_{1}} ,\ensuremath{{\bf p}_{2}} ;\ensur... ...}} ) = \frac{\Delta_{13}\Delta_{24}}{\Delta_{14}\Delta_{23}}.$$ (2)

In other words, select one of the points, say $\ensuremath{{\bf p}_{1}}$, to be a reference point. Compute the ratio of distances from that point to two other points, say $\ensuremath{{\bf p}_{3}}$ and $\ensuremath{{\bf p}_{4}}$. Then compute the ratio of distances from the remaining point, in this case $\ensuremath{{\bf p}_{2}}$, to the same two points. The ratio of these ratios is invariant under projective transformations.

The Euclidean distance between two points $\ensuremath{{\bf p}_{i}} =[X_i,Y_i,W_i]^T$and $\ensuremath{{\bf p}_{j}} =[X_j,Y_j,W_j]^T$ is computed from the 2D Euclidean points obtained by dividing by the third coordinate, as mentioned in section 2.1.1:

$$\Delta_{ij} = \sqrt{\left(\frac{X_i}{W_i}-\frac{X_j}{W_j}\right)^2 + \left(\frac{Y_i}{W_i}-\frac{Y_j}{W_j}\right)^2}.$$

Actually, the cross ratio is the same no matter which coordinate is used as the divisor (as long as the same coordinate is used for all the points); thus, if all the points lie on the ideal line (W_i=0 for all i), then we can divide by X_i or Y_i instead. For a set of collinear points, we can always select a coordinate such that at least three of the points have nonzero entries for that coordinate. If one of the points has a zero entry, simply cancel the terms containing the point (because it lies at infinity); for example, if the second point is the culprit (W₂=0; $W_1,W_3,W_4\ne0$), then $\Delta_{23} = \Delta_{24} = \infty$, which cancel each other:

$$Cr(\ensuremath{{\bf p}_{1}} ,\ensuremath{{\bf p}_{2}} ;\ensur... ...\ensuremath{{\bf p}_{4}} ) = \frac{\Delta_{13}}{\Delta_{14}}.$$

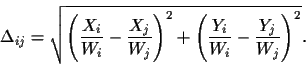
Although the cross ratio is invariant once what the order of the points has been chosen, its value is different depending on that order. Four points can be chosen 4! = 24 ways, but in fact only six distinct values are produced, which are related by the set

$$\{\tau, \frac{1}{\tau}, 1-\tau, \frac{1}{1-\tau}, \frac{\tau-1}{\tau}, \frac{\tau}{\tau-1}\}.$$

As we hinted before, there are other measures of the cross ratio, all of which are also invariant under projective transformations. Not surprisingly, duality leads to a cross ratio for four concurrent lines by replacing the Euclidean distance between two points with the sine of the angle between two lines (I have not confirmed whether the cosine also works). Another less obvious way to measure the cross ratio between four concurrent lines is to use a new, arbitrary line that intersects them; the cross ratio of the lines is then defined as the cross ratio of the four points of intersection (The cross ratio will be the same no matter which line is used).

As a final comment on the cross ratio, it is worth noting that it does not require that the original points be collinear. For example, given five points in a star configuration, as shown in figure 6, we can connect the dots as shown in (a) to yield lines containing four collinear points, the points of intersection, whose cross ratio can be used. Another possibility is to draw lines from one of the points to the other four, as shown in (b), thus yielding four concurrent lines whose cross ratio can be used.

  

Figure 6: The cross ratio can be used with five noncollinear points.