Homogeneous coordinates

Suppose we have a point (x,y) in the Euclidean plane. To represent this same point in the projective plane, we simply add a third coordinate of 1 at the end: (x, y, 1).¹ Overall scaling is unimportant, so the point (x,y,1) is the same as the point $(\alpha x, \alpha y, \alpha)$, for any nonzero $\alpha$. In other words,

$$(X,Y,W) = (\alpha X, \alpha Y, \alpha W)$$

for any $\alpha \neq 0$ (Thus the point (0,0,0) is disallowed). Because scaling is unimportant, the coordinates (X,Y,W) are called the homogeneous coordinates of the point. In our discussion, we will use capital letters to denote homogeneous coordinates of points, and we will use the coordinate notation (X,Y,W)interchangeably with the vector notation [X,Y,W]^T.

To represent a line in the projective plane, we begin with a standard Euclidean formula for a line

ax+by+c = 0,

and use the fact that the equation is unaffected by scaling to arrive at the following:

aX+bY+cW = 0

$$\ensuremath{{\bf u}} ^T \ensuremath{{\bf p}} = \ensuremath{{\bf p}} ^T \ensuremath{{\bf u}}$$ = 0, (1)

where $\ensuremath{{\bf u}} = [a,b,c]^T$ is the line and $\ensuremath{{\bf p}} =[X,Y,W]^T$ is a point on the line. Thus we see that points and lines have the same representation in the projective plane. The parameters of a line are easily interpreted: -a/b is the slope, -c/a is the x-intercept, and -c/b is the y-intercept.

To transform a point in the projective plane back into Euclidean coordinates, we simply divide by the third coordinate: (x,y) = (X/W, Y/W). Immediately we see that the projective plane contains more points than the Euclidean plane, that is, points whose third coordinate is zero. These points are called ideal points, or points at infinity. There is a separate ideal point associated with each direction in the plane; for example, the points (1,0,0) and (0,1,0) are associated with the horizontal and vertical directions, respectively. Ideal points are considered just like any other point in $\ensuremath{{\cal P}^2}$ and are given no special treatment. All the ideal points lie on a line, called the ideal line, or the line at infinity, which, once again, is treated just the same as any other line. The ideal line is represented as (0,0,1).

Suppose we want to find the intersection of two lines. By elementary algebra, the two lines $\ensuremath{{\bf u}_{1}} = (a_1,b_1,c_1)$ and $\ensuremath{{\bf u}_{2}} = (a_2,b_2,c_2)$ are found to intersect at the point $\ensuremath{{\bf p}} = (b_1c_2-b_2c_1,a_2c_1-a_1c_2,a_1b_2-a_2b_1)$. This formula is more easily remembered as the cross product: $\ensuremath{{\bf p}} = \ensuremath{{\bf u}_{1}}\times \ensuremath{{\bf u}_{2}}$. If the two lines are parallel, i.e., -a₁/b₁ = -a₂/b₂, the point of intersection is simply (b₁c₂-b₂c₁,a₂c₁-a₁c₂,0), which is the ideal point associated with the direction whose slope is -a₁/b₁. Similarly, given two points $\ensuremath{{\bf p}_{1}}$ and $\ensuremath{{\bf p}_{2}}$, the equation of the line passing through them is given by $\ensuremath{{\bf u}} = \ensuremath{{\bf p}_{1}}\times \ensuremath{{\bf p}_{2}}$.

Now suppose we want to determine whether three points $\ensuremath{{\bf p}_{1}}$, $\ensuremath{{\bf p}_{2}}$, and $\ensuremath{{\bf p}_{3}}$ lie on the same line. The line joining the first two points is $\ensuremath{{\bf p}_{1}}\times \ensuremath{{\bf p}_{2}}$. The third point then lies on the line if $\ensuremath{{\bf p}_{3}} ^T (\ensuremath{{\bf p}_{1}}\times \ensuremath{{\bf p}_{2}} ) = 0$, or, more succinctly, if the determinant of the $3 \times 3$ matrix containing the points is zero:

$$\det \left[\matrix{\ensuremath{{\bf p}_{1}} & \ensuremath{{\bf p}_{2}} & \ensuremath{{\bf p}_{3}} }\right] = 0.$$

Similarly, three lines $\ensuremath{{\bf u}_{1}}$, $\ensuremath{{\bf u}_{2}}$, and $\ensuremath{{\bf u}_{3}}$ intersect at the same point (i.e., they are concurrent), if the following equation holds:

$$\det \left[\matrix{\ensuremath{{\bf u}_{1}} & \ensuremath{{\bf u}_{2}} & \ensuremath{{\bf u}_{3}} }\right] = 0.$$

The concepts of homogeneous coordinates are summarized in Figure 2. For further reading, consult the notes by Guibas [3].

Example 1. Given two lines $\ensuremath{{\bf u}_{1}} = (4,2,2)$ and $\ensuremath{{\bf u}_{2}} = (6,5,1)$, the point of intersection is given by:

$$\left\vert\matrix{\ensuremath{{\bf i}} & \ensuremath{{\bf j}}... ...h{{\bf j}} +(20-12)\ensuremath{{\bf k}} = (-8,8,8) = (-1,1,1).$$

  

Figure 2: Summary of homogeneous coordinates: (a) points, and (b) lines.

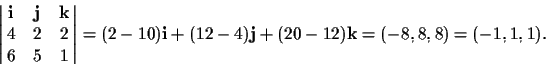
Example 2. Consider the intersection of the hyperbola xy=1 with the horizontal line y=1. To convert these equations to homogeneous coordinates, recall that X=Wx and Y=Wy, yielding XY=W² for the hyperbola and Y=W for the line. The solution to these two equations is the point (W,W,W), which is the same as the point (1,1) in the Euclidean plane, the desired result. Now let us consider the intersection of the same hyperbola with the horizontal line y=0, an intersection which does not exist in the Euclidean plane. In homogeneous coordinates the line becomes Y=0 which yields the solution (X,0,0), the ideal point associated with the horizontal direction.