Essential and fundamental matrices

Suppose we have a stereo pair of cameras viewing a point $\ensuremath{{\bf M}}$ in the world which projects onto the two image planes at $\ensuremath{{\bf\bar m}} _1$ and $\ensuremath{{\bf\bar m}} _2$ (Since we are dealing with homogeneous coordinates, $\ensuremath{{\bf M}}$ is $4 \times 1$, and $\ensuremath{{\bf\bar m}} _1$ and $\ensuremath{{\bf\bar m}} _2$ are each $3 \times 1$). If we assume the cameras are calibrated, then $\ensuremath{{\bf\bar m}} _1$ and $\ensuremath{{\bf\bar m}} _2$ are given in normalized coordinates, that is, each is given with respect to its camera's coordinate frame. The epipolar constraint says that the vector from the first camera's optical center to the first imaged point, the vector from the second optical center to the second imaged point, and the vector from one optical center to the other are all coplanar. In normalized coordinates, this constraint can be expressed simply as

$$\ensuremath{{\bf\bar m}} _2^T(\ensuremath{{\bf t}}\times R \ensuremath{{\bf\bar m}} _1) = 0,$$

where R and $\ensuremath{{\bf t}}$ capture the rotation and translation between the two cameras' coordinate frames. The multiplication by R is necessary to transform $\ensuremath{{\bf\bar m}} _1$ into the second camera's coordinate frame. By defining $[\ensuremath{{\bf t}} ]_x$ as the matrix such that $[\ensuremath{{\bf t}} ]_x \ensuremath{{\bf y}} = \ensuremath{{\bf t}}\times \ensuremath{{\bf y}}$ for any vector $\ensuremath{{\bf y}}$,⁴ we can rewrite the equation as a linear equation:

$$\ensuremath{{\bf\bar m}} _2^T([\ensuremath{{\bf t}} ]_x R \en... ...nsuremath{{\bf\bar m}} _2^T E \ensuremath{{\bf\bar m}} _1 = 0,$$

where $E = [\ensuremath{{\bf t}} ]_x R$ is called the Essential matrix and has been studied extensively over the last two decades.

Now suppose the cameras are uncalibrated. Then the matrices A₁ and A₂ (from (4)) containing the internal parameters of the two cameras are needed to transform the normalized coordinates into pixel coordinates:

$$\begin{eqnarray*}\ensuremath{{\bf m}} _1 & = & A_1 \ensuremath{{\bf\bar m}} _1 \\ \ensuremath{{\bf m}} _2 & = & A_2 \ensuremath{{\bf\bar m}} _2. \end{eqnarray*}$$

This yields the following equation:

 

$$(A_2^{-1} \ensuremath{{\bf m}} _2)^T(\ensuremath{{\bf t}}\times R A_1^{-1} \ensuremath{{\bf m}} _1)$$ = 0

$$\ensuremath{{\bf m}} _2^T A_2^{-T}(\ensuremath{{\bf t}}\times R A_1^{-1} \ensuremath{{\bf m}} _1)$$ = 0 (6)

$$\ensuremath{{\bf m}} _2^T F \ensuremath{{\bf m}} _1$$ = 0, (7)

where F = A₂^-T E A₁^-1 is the more recently discovered Fundamental matrix.

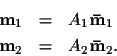
Thus both the Essential and Fundamental matrices completely describe the geometric relationship between corresponding points of a stereo pair of cameras. The only difference between the two is that the former deals with calibrated cameras, while the latter deals with uncalibrated cameras. The Essential matrix contains five parameters (three for rotation and two for the direction of translation -- the magnitude of translation cannot be recovered due to the depth/speed ambiguity) and has two constraints: (1) its determinant is zero, and (2) its two non-zero singular values are equal. The Fundamental matrix contains seven parameters (two for each of the epipoles and three for the homography between the two pencils of epipolar lines) and its rank is always two [4].

There are several other ways to derive the Essential and Fundamental Matrices, each of which presents a little more insight into their nature. In the next few subsections, we will look at these methods and then summarize our findings.