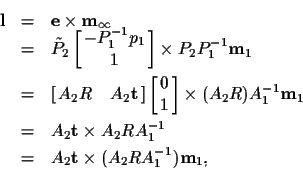

Next: Summary
Up: Essential and fundamental matrices
Previous: Alternate derivation: algebraic
Faugeras [2] approaches the problem from a slightly
different direction by using the fact that the point
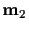 must lie on the epipolar line corresponding to
must lie on the epipolar line corresponding to
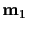 :
:
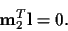 |
(11) |
That line contains two points, the epipole
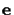 (the projection of the first camera's optical center
into the second camera)
and the point at infinity
associated with
(the projection of the first camera's optical center
into the second camera)
and the point at infinity
associated with
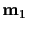 :
:
In [2, pp. 40-41] it is shown that the epipole is
given by
and the point at infinity by
Therefore, the epipolar line is:
where we have used the substitutions in (5).
Combining with (11), we get the desired result:
Stanley Birchfield
1998-04-23
![]() must lie on the epipolar line corresponding to
must lie on the epipolar line corresponding to
![]() :
: