An interface endowed with surface tension can reconfigure itself in the form of a number of classical hydrodynamic instabilities; capillary-gravity waves, Faraday waves, Plateau-Rayleigh break-up of a fluid cylinder, buoyancy-driven Rayleigh-Taylor instability, and Kapitza waves on thin films. These instabilities often exhibit a dispersion relationship from which the dominant pattern emerges. Introducing a solid support affects the pattern formation, e.g. a liquid cylinder constrained by a plane is a rivulet and when constrained by a cylinder is a bead-on-fiber. Similar instabilities have been observed on complex fluids and soft gels.

• 

• 

• 

Bead-on-fiber

A thin film flowing down a fiber exhibits a bead-on-fiber morphology and instabilities characterized by i) isolated bead formation, ii) Plateau-Rayleigh instability, and iii) convective instability (cf. Figure above (left)). For liquids with small surface tension, e.g. silicone oil, the instability is symmetric about the fiber, but for liquids with high surface tension, e.g. glycerol/water mixtures, the instability is asymmetric about the fiber and the two configurations exhibit much different dynamics. When the working liquid is a complex fluid, the dispersion relationship also depends upon the rheology.

Interfacial waves

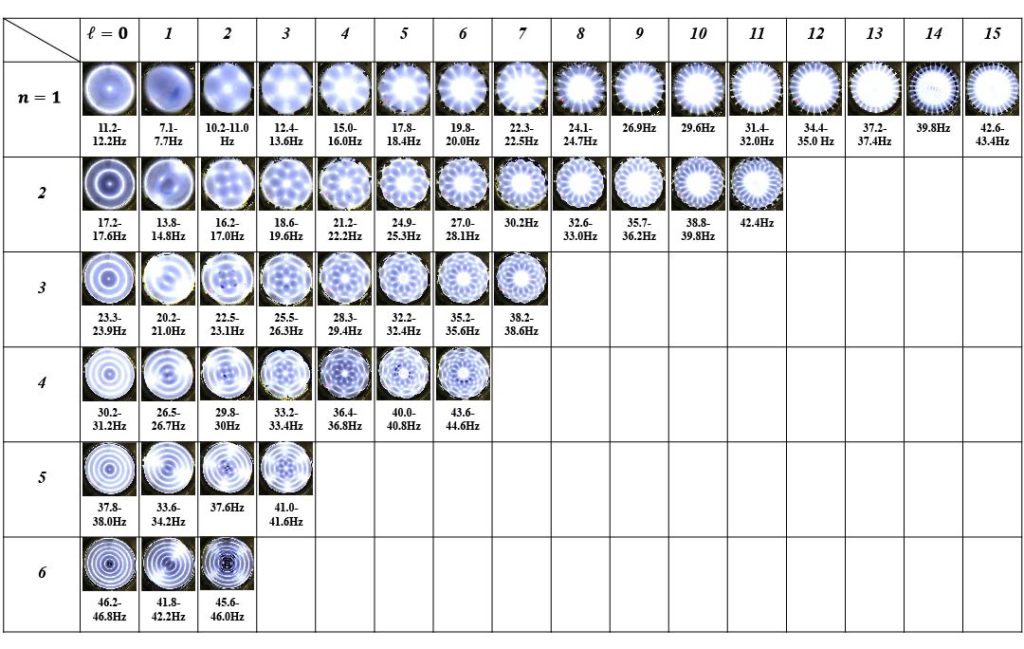
Capillary-gravity waves are formed on a flat interface through mechanical vibration of the liquid bath. For small containers, the waves conform to the geometry of the container, e.g. for a cylindrical container the modes are characterized by a radial mode number n and polar mode number l. The dynamic response of the wave is closely related to the contact conditions at the container sidewall; whenever the meniscus is not perfectly flat, harmonic edge waves are excited for any driving amplitude, but when the meniscus is flat, edge waves are suppressed and Faraday waves with a subharmonic response can be excited above the threshold forcing amplitude. The Figure below is a catalogue of Faraday waves in a cylindrical container. Mode mixing can occur for interfaces that are not perfectly flat in which both edge waves and Faraday waves can be excited at the same driving frequency.

• 

Elastocapillary waves and instabilities

Numerous interfacial instabilities have been observed in soft gels including Rayleigh-Taylor, Plateau-Rayleigh, Faraday, and elastocapillary waves. These all involve elastocapillary effects, which involve the effects of elasticity and surface tension of the interface. Typically, there is a crossover between capillary-dominated and elasticity-dominated dynamics and this occurs whenever the elastocapillary length is comparable to the characteristic length of the system, i.e. wavelength of the surface wave, radius of a drop, or thickness of the thin film.

•