Transport of liquids on soft substrates is critical to many biological and medical applications, such as drug delivery systems. Yet, despite its importance, the most basic characterization of how liquids wet soft solids is not well understood, because, in contrast to rigid substrates, surface tension forces can deform soft solids. With regards to materials science, small surface tension forces can be used in lieu of conventional measurement techniques to probe the mechanical properties of soft solids.
Wetting ridge (statics)
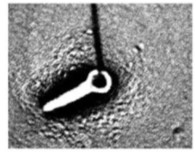
A static drop resting on a soft substrate deforms the contact-line into a wetting ridge of size defined by the elastocapillary length δ ∼ σ/E. For reference, water (σ=72mN/m) on a glass substrate (E=70GPa) has δ ∼ 10-12m, justifying the neglect of substrate elasticity, but for silicone gels (E=3 kPa) δ ∼ 10-6m and the substrate deforms into the wetting ridge (cf. Figure). The shape of the wetting ridge is determined by the elastic response of the substrate due to the wetting interactions from the drop and the intrinsic surface energies of the substrate. For a spreading drop on a viscoelastic substrate, the three-phase contact-line and the wetting ridge exhibit their own dynamics leading to complex spreading behaviors such as viscoelastic braking, stick-slipping, and stick-breaking.
Experimental image of wetting ridge (courtesy of S. Park) 
Theoretical predictions of the shape of the wetting ridge
Droplet durotaxis
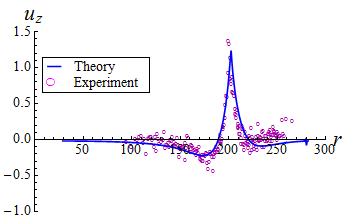
It has been recently shown that a liquid droplet can be spontaneously transported across a soft substrate with gradient in thickness. This passive transport mechanism is referred to as droplet durotaxis. Here the asymmetry in shape of the wetting ridge at the advancing and receding contact-lines gives rise to a net wetting force responsible for transport whose velocity is largely determined by balancing the work done by this force with the energy dissipated by the viscoelastic substrate and liquid droplet during spreading.
Soft fracture
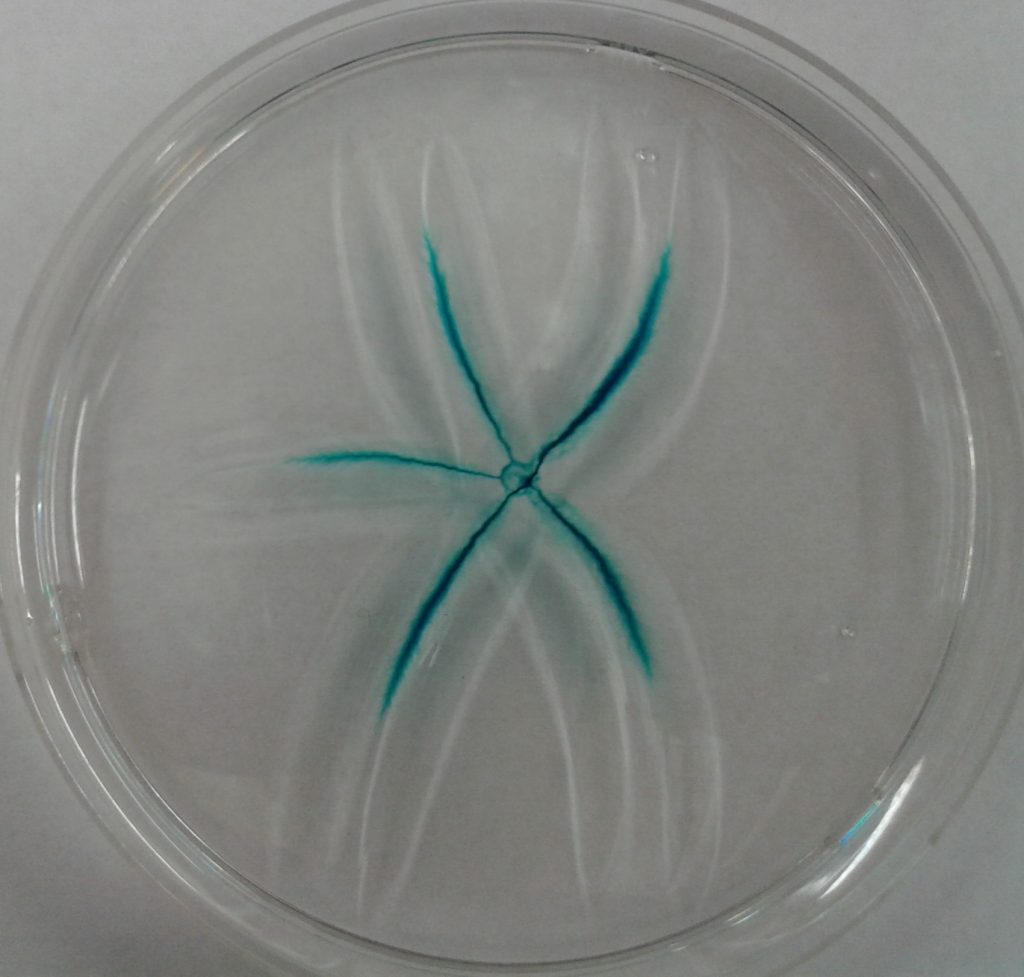
If the substrate is sufficiently `soft’, e.g. agarose gel (E~10Pa), δ∼10-3m can be of millimetric size . To put this length scale into perspective, note that to produce millimeter size deformations on a glass substrate one would have to load the substrate with the weight of 40 Mini Coopers spaced evenly along a 1mm ring. Not surprisingly, such deformations can cause material failure in which fractures develop on the gel surface and propagate outwards from the contact-line in a starburst pattern (cf. Figure). The fracture process can be conveniently divided into three phases; 1) initation, 2) nucleation and 3) propagation. There is an inherent variability in both the number of fractures formed and the time delay before fractures form, which exhibits a Weibull-like distribution consistent with a thermally-activated process. By looking at the statistics, it is possible to probe the energy landscape and fracture toughness of ultrasoft materials through measurement of the delay time distribution.
Starburst fracture on agarose gel 
Delayed fracture
Splashing on soft substrates
Aerosol drug delivery relies upon the impaction of liquid droplets with soft biological tissues. This is the classic drop splash problem in which the drop inertia is transformed into dynamic wetting and interfacial shape change leading to the formation of satellite drops during pinchoff. When the substrate is soft, the initial kinetic energy is partitioned into liquid shape change and elastic deformation, resulting in splash suppression, arrested spreading, and a complex relationship for the spine number that depends upon the elasticity and substrate wetting properties.
Elastocapillary instabilities (dynamics)
Elastocapillary effects are also seen in the interfacial deformations of soft materials, whenever the intrinsic surface tension and elasticity of the material are comparable in magnitude. In fact, many of the classic interfacial instabilities of fluid mechanics have been observed in soft materials; Rayleigh-Taylor instability, Plateau-Rayleigh instability, Faraday waves, and Rayleigh drop oscillations. These problems are challenging to analyze because they are dynamic and involve the inherent time scales associated with capillarity, elasticity, and viscoelastic relaxation.